1910. Empire
The
Empire consists of n planets. Lets
label these planets with numbers from 1 to n.
The planet with the number 1 is a capital of Empire, where the Emperor
residence is located and the troops are prepared. On different planets of the
empire the uprisings are often, which must be suppressed by force and
immediately.
In
order for troops to move quickly, the one-way teleports are installed on some
planets. There are m teleports in total. Using the i-th teleport you can get instantly from planet ai to planet bi (but not vice versa).
Thus, it is possible to crush the rebellion in time on some planet x, if there is a sequence of planets p1, ..., pk
(k ≥ 2) such that p1 = 1, pk = x, and
for each 1 ≤ i < k there is a teleport from planet with
number pi to the planet
with number pi+1.
After crushing the uprising, the troops remain on the planet to maintain the
order, so we do not need to worry about their return to the capital.
Check
is there an opportunity using the existing system of teleports to crush the
rebellion on any planet of the Empire. If so, print 0. Otherwise find the
minimum number of teleports that must be built more so that the rebellion on
any planet can be suppressed instantly. Each new teleport can be constructed
between any two planets.
Input. The first
line contains two integers n and m (2 ≤ n ≤ 105, 0 ≤ m ≤ 2·105). The i-th of the next m lines
contains the pair of numbers ai,
bi (1 ≤ ai, bi ≤ n)
for all 1 ≤ i ≤ m. No one planet has a teleport to
itself. No one planet has two teleports to the same planet.
Output.
Print the minimum number of teleports, ensuring that the revolt on any planet
can be immediately suppressed.
|
Sample
input |
Sample
output |
6 43 14 61 2
4 5 |
2 |
SOLUTION
graphs – strong connected
components
Algorithm analysis
In the graph
representing the empire, add the least number of edges so that any vertex is
reachable from vertex 1 (the capital).
Note that new edges can only be constructed from the first
vertex. Indeed, if the new arc is (a,
b), then replacing it with (1, b), we will not change the reachability
of the vertices from the capital.
Consider a graph
condensation and choose a vertex that does not have incoming edges (the condensation graph is
acyclic, such vertices always exist). Some strongly connected component
corresponds to this vertex. From vertex 1 it is necessary to construct an edge to one of the
vertices of this strongly connected component. There is one exception here – if vertex 1 itself is included in this
strongly connected component, then no edge need to be constructed.
If in the
condensation graph there are edges incoming to the vertex v, then there is no need to construct new edges in
the original graph from vertex 1 to the vertices of the strongly connected
component corresponding to v.
Thus, in this problem it is
necessary to find the number of strongly connected components into which there is no incoming edges in
condensation graph. The component that contains the capital should be processed
separately.
Example
Graph given in a sample, has the form:
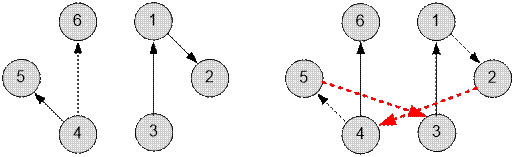
To solve the
problem, it is enough to build two additional teleports. You can, for example,
build a teleport from planet 2 to planet 4 and from planet 5 to planet 3.
The given graph has 6
strongly connected components: each vertex forms a separate component. Find the
components without
incoming edges. There will be two of them: those that contain vertices 3 and 4.
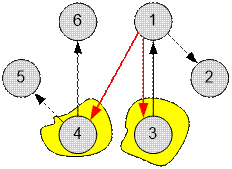
Thus, it is
enough to build two new teleports from the capital (vertex 1), running respectively to
vertices 3 and 4.
Algorithm realization
Represent the
empire as a graph and store it in an adjacency list g.
Store the
transposed graph in the adjacency list gr.
The array used is used to mark the already visited vertices, top for topological sorting of the vertices, and color for coloring the vertices
according to their occurrence in the strongly connected components.
vector<vector<int> > g, gr;
vector<int> used, top, color;
The function dfs1 implements
depth first search on the input graph. In the array top store the
vertices in the order in which the depth first search ends their
processing.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs1(to);
top.push_back(v);
}
The function dfs2 implements
depth first search on the reversed graph. Color all the vertices
of the strongly connected component that contains v with color c.
void dfs2(int v, int c)
{
color[v] = c;
for (int to : gr[v])
if (color[to] == -1) dfs2(to,
c);
}
The main part of
the program. Read the input
data and build the graph of empire g.
Simultaneously construct the reversed graph gr.
scanf("%d %d",&n,&m);
g.resize(n+1);
gr.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
gr[b].push_back(a);
}
Start the first depth first search on the
graph. Sort topologically the vertices of the
graph in the array top.
used.resize(n+1);
for(i = 1; i <= n; i++)
if (!used[i])
dfs1(i);
Color the vertices. The vertices included in one strongly connected component are colored with the same color. The
current color is in the variable c.
color.assign(n+1,-1);
c = 0;
for(i = 1; i <= n; i++)
{
v = top[n-i];
if (color[v]
== -1) dfs2(v,c++);
}
The value of c equals to the number of strongly
connected components and equals to the number of vertices in the condensation of the graph. Compute the number of connected components without
incoming edges in the condensation graph. Set used[c] = 0, if it
is not required to create a new edge from the capital to the
vertices colored with color c. Such
color ñ will be called useless.
used.assign(c,1);
for(i = 1; i < g.size(); i++)
for (int to : g[i])
For each edge (i, to), check whether the vertices i and to are in different strongly connected components.
If so, then declare color color[to]
as useless.
if (color[i] !=
color[to]) used[color[to]] = 0;
There is no need to create an edge from the first vertex (capital) to the vertex of the
connected component where the capital is located. Therefore, let’s mark the color of the capital as useless (even if it may
have already been marked as such before).
used[color[1]] =
0;
Compute and print the number of strongly connected components without
incoming edges in the condensation graph.
c = 0;
for(i = 0; i < used.size(); i++)
if (used[i])
c++;
Print the answer.
printf("%d\n",c);
Java realization
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g, gr;
static int used[], color[];
static
Vector<Integer> top = new
Vector<Integer>();
static void
dfs1(int v)
{
used[v] =
1;
for(int i = 0;
i < g[v].size();
i++)
{
int to = g[v].get(i);
if (used[to] ==
0) dfs1(to);
}
top.add(v);
}
static void
dfs2(int v, int c)
{
color[v] = c;
for(int i = 0;
i < gr[v].size();
i++)
{
int to = gr[v].get(i);
if (color[to] ==
-1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new
ArrayList[n+1];
for(int i = 0;
i <= n; i++)
g[i] = new
ArrayList<Integer>();
gr = new
ArrayList[n+1];
for(int i = 0;
i <= n; i++)
gr[i] = new
ArrayList<Integer>();
for (int i = 0;
i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n+1];
for(int i = 1;
i <= n; i++)
if (used[i] ==
0) dfs1(i);
color = new int[n+1];
Arrays.fill(color,
-1);
int c = 0;
for(int i = 1;
i <= n; i++)
{
int v = top.get(n-i);
if (color[v] ==
-1) dfs2(v,c++);
}
used = new int[c];
Arrays.fill(used, 1);
for(int i = 1;
i < g.length; i++)
for(int j = 0;
j < g[i].size();
j++)
{
int to = g[i].get(j);
//
check edge i -> j if they in the same scc.
if (color[i] != color[to]) used[color[to]] =
0;
}
used[color[1]]
= 0;
c = 0;
for(int i = 0;
i < used.length; i++)
if (used[i] ==
1) c++;
System.out.println(c);
con.close();
}
}